Machine Learning Meets Clinical Trials: Harmonizing Data with Reality
Mitigating the Impact of Dataset Shift in Machine Learning and External Validity Deficit in Clinical Trials

An article published this week in the New England Journal of Medicine (NEJM) by Andrew S. Lea, MD, DPhil and David S. Jones, MD, PhD called "Mind the Gap - Machine Learning, Dataset Shift, and History in the Age of Clinical Algorithms" delves into the challenges of implementing machine learning for biomedical applications, focusing on the issue of dataset shift. It begins with a historical context, examining AAPHelp, a computational system developed by the British surgeon Francis Timothy de Dombal at the University of Leeds in the 1970s. The system was designed for diagnosing acute abdominal pain, utilizing the principle of Bayes theorem. The underpinnings of the effort were anchored on the principles pioneered by Robert S. Ledley and Lee E. Lusted who’s work and the 1959 Science paper “Reasoning Foundations of Medical Diagnosis: Symbolic logic, probability, and value theory aid our understanding of how physicians reason” helped lay the foundation of the modern field of bioinformatics. AAPHelp demonstrated high diagnostic accuracy in its original setting at Leeds, with an impressive 92% accuracy “surpassing the performance of senior clinicians.1” However, its performance declined to 65% outside of Leeds due to the phenomenon of dataset shift.
Dataset shift, as the NEJM article explains, is the mismatch between the data on which a machine learning model is trained or tested and the actual population it is applied to. This shift can arise from various factors such as differences in patient demographics, clinical presentations, and classification methods. The system's decreased accuracy in new clinical settings was attributed to wide variations in the clinical presentation of diseases that can lead to acute abdominal pain and the differing methods of symptom description and classification.
As the article states, the challenge of dataset shift is still pertinent in modern medicine, especially as machine learning algorithms are increasingly integrated into biomedical research and clinical practice. But the problem is not limited to machine learning as it can afflict even the most trusted sources of clinical evidence: the results of traditional clinical trials.

Dataset Shift: A Closer Examination
Before I delve into how the results of clinical trials can suffer from a phenomenon analogous to dataset shift, it’s beneficial to expand on the concept of dataset shift.
Dataset shift (Table 1) in machine learning refers to situations where the data distribution a model is trained on differs from the data it encounters in real-world applications. This shift can lead to decreased accuracy and reliability of the model when applied to new datasets. The related concept of conditional distribution plays a key role in the process and defined as the distribution of a variable given the presence of other variables. This is important in understanding complex relationships in data as it can influence the accuracy of machine learning models in predicting outcomes based on a set of conditions. For example, the graph below shows the conditional distribution of Blood Pressure (BP) across different Age Groups. Each subplot represents a different age group, with BP values plotted on the x-axis and their frequency on the y-axis. This visualization helps in understanding how the distribution of BP (a feature) varies conditionally on the Age Group (another feature).
As seen above, the central tendency (mean/average) of BP appears to increase with age and there's also a slight increase in the spread (variance) of the values. Understanding these relationships between variables in populations of interest is essential for making informed decisions on developing machine learning models (and designing clinical trials as I explain later).
Dataset shift can be characterized in several ways, depending on the nature of the changes between the training and testing data, as shown below.
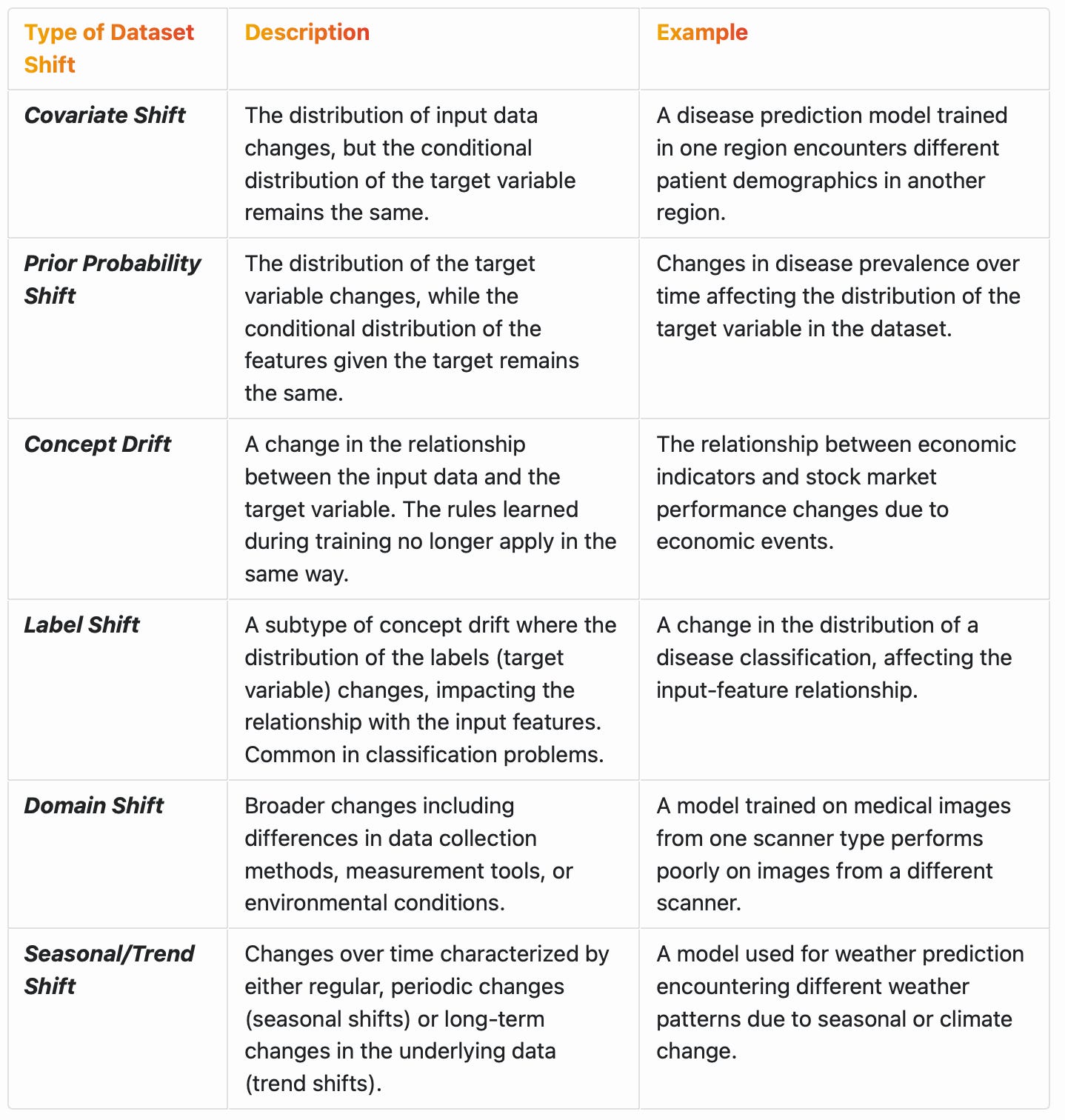
In some cases, dataset shift can be a consequence of changes in the conditional distribution of variables. For example, in concept drift, the relationship between the input variables and the target variable changes, which means the conditional distribution of the target given the inputs changes.2 In other forms of dataset shift, like covariate shift, the conditional distribution of the output given the input does not change, but the distribution of the input variables themselves changes.3
In developing machine learning models, recognizing changes in conditional distributions can help in adapting the models to new data or in applying techniques like re-weighting to adjust for the shift.
The Connection Between Dataset Shift and External Validity in Clinical Trials
Dataset shift in machine learning is analogous to external validity deficits in clinical trials. External validity refers to the extent to which the results of a study can be generalized or applied beyond the specific conditions, context, or population in which the study was conducted. It’s a measure of how well the findings of a clinical trial can be expected to hold true for real-world patient populations. External validity deficits in clinical trials can arise from differences between clinical trial and real-world patients due to factors that include narrow eligibility criteria and socioeconomic barriers to study participation. The most precise mathematical rationale I can think of in support of the use of real-world evidence in therapeutic development is to address the external validity deficits of traditional clinical trials.
In both dataset shift and external validity deficits, there's a gap between the conditions or populations for which the model or the trial was developed and those it is eventually applied to. My colleague, Roger Stein, PhD and I, developed a simple mathematical method for clinicians without expertise in probability calculations to adjust the results of traditional clinical trials to make them more relevant to their patients at the point of care. Recognizing the importance of conditional distributions in this context, it’s imperative to give them increased attention when designing clinical trials that strike an appropriate balance between internal and external validity. For example, by quantifying how outcomes may differ across various subpopulations or conditions, we can improve the generalizability of the findings through the implementation of suitable, and in many cases broader, patient selection criteria. In a recent study, we examined the impact of broadening eligibility criteria for cancer clinical trials using real-world data based on the official recommendations of ASCO and Friends of Cancer Research. We noted that broadening eligibility criteria would enable more equitable patient involvement in clinical research, accelerate trial enrollment, and increase the external validity of trial results.
Mathematical Representation of Dataset Shift and External Validity
[Please feel free to skip this section]
Let’s express dataset shift and external validity mathematically. In a previous post, I explained how machine learning is basically a mathematical function optimization process expressed as y = f(x) where y is the output (dependent variable or prediction) and f is the machine learning model applied to the input (independent) variable x. During training, the machine learning model learns from a training dataset and when the model is tested or applied in the real world, it encounters new data for predicting y. The joint probability distribution of inputs x and outputs y in the training and test data can be denoted as:
This distribution encompasses all the patterns, relationships, and characteristics the model learns. Dataset shift occurs when there is a discrepancy between these two distributions. Mathematically, this can be expressed as:
This overarching concept can be broken down into specific types of shift. For example, in the case of covariate shift, the shift is in the distribution of inputs x, meaning:
But, despite the shift in x, the conditional distribution of y given x remains the same4:
Quantitatively measuring this shift can involve various statistical techniques. One common approach is using divergence metrics like the Kullback-Leibler (KL) divergence, which measures how one probability distribution diverges from a second, expected probability distribution.
External validity deficits in clinical trials follow a similar logic, occurring, for example, when point estimates for the effect size (E) in a clinical trial is approximately5 different than that observed in the real world:
The Need for Global Harmonization: Addressing Dataset Shift in Machine Learning and External Validity Deficits in Clinical Trials
The harmonization of data collection standards and procedures in clinical trials and at the point of care in different regions and time periods can address both dataset shift and external validity deficits. By standardizing methodologies, measurement tools, and data reporting practices, harmonization ensures that data from diverse sources (and the results, or predictions based on them) are comparable and comprehensive. This approach is essential in creating datasets that accurately reflect broader patient populations and real-world conditions, thereby minimizing bias and enhancing the external validity of clinical trials and reducing dataset shift in machine learning models. Harmonization can also aid in meeting the diverse regulatory requirements of different countries. Regulatory agencies such as the US Food and Drug Administration (FDA), European Medicines Agency (EMA), and others often have specific guidelines for the generation of clinical evidence in support of approval decisions. A harmonized approach simplifies the compliance process, making it more straightforward to generate robust datasets and seek approval in multiple markets with efficiency while enabling optimal conditions for applying machine learning methods for secondary analyses of the data.
A global approach to clinical trial data harmonization and real-world data collection and analysis faces several challenges, including variability in healthcare systems, differences in regulatory and ethical standards, and the need for sophisticated data infrastructure. However, initiatives such as HARMONY have demonstrated the feasibility and benefits of such an approach. HARMONY is an initiative (which I’m involved in) focused on creating a unified, global approach to cancer clinical trials. It exemplifies how harmonization can address external validity deficits and dataset shift challenges while lowering barriers in access to potentially lifesaving experimental therapies, especially in underserved communities.
HARMONY highlights the significance of a harmonized approach in integrating real-world data and evidence into decision-making frameworks, thereby enhancing the relevance and applicability of clinical evidence for new therapies. This method aligns with the overarching goals of global harmonization in biomedical research, focusing on the development of equitable, efficient, and universally applicable research standards. By ensuring that clinical trial evidence is representative of a wide range of patient populations and by improving access to comprehensive real-world datasets, such efforts can contribute to the acceleration of clinical trials while improving the applicability of the results. This approach can effectively mitigate external validity deficits in clinical trials and facilitates the generation of data that’s optimally tailored for machine learning applications, thereby minimizing the likelihood of dataset shift.
Lea, A. S. & Jones, D. S. Mind the Gap — Machine Learning, Dataset Shift, and History in the Age of Clinical Algorithms. New England Journal of Medicine (2024).
This can be shown when, over time, the manifestation of diseases evolves. For instance, the presentation and progression of certain cancers might change due to environmental factors or evolving lifestyles. A model trained to predict cancer outcomes based on historical data may lose accuracy over time as the relationship (conditional distribution) between the input variables (symptoms, patient demographics) and the target variable (cancer progression) changes. In addition, as new treatments are introduced and become standard practice, the relationship between patient characteristics (inputs) and treatment outcomes (output) may change. A predictive model developed under old treatment protocols might not be accurate under new protocols.
An example is how advances in diagnostics like a digital BP measurement tool or new medical imaging technology might change the characteristics of the input data (e.g., continuous BP measurements and higher resolution images, respectively). A model trained on data from older BP monitors or imaging technology might not perform well on data from newer technology, even if the underlying conditional distributions (e.g., BP measurements by age group) remains the same.
In probability theory, | is used in the context of conditional probability. For example, P(A|B) denotes the probability of event A given that event B has occurred.
We say approximately here because we never expect the results of clinical trials to exactly mirror observations in the real-world.



