The End of Disciplinary Sovereignty

Rethinking Expertise in the Era of Algorithmic Intelligence

Preface: On mathematical fluency in the age of AI

Throughout this essay, I use "mathematical fluency" to mean something specific: not manual derivations or rote memorization, but structural literacy—the ability to recognize when seemingly disparate problems share the same underlying mathematical form. This kind of fluency becomes essential as AI systems increasingly handle technical workloads, leaving humans to identify abstract patterns, reason across formal systems, and translate models into real-world interventions.

Understanding that a clinical trial and a portfolio optimization problem are both forms of decision-making under uncertainty, constrained by resources, time, and ethical limits—this is the fluency that matters as AI makes the technical more accessible and the conceptual more decisive

---

By all conventional measures, my career might appear improbable. I trained as a physician-scientist and oncologist, immersed in the world of cellular pathways and clinical trials. I design AI/ML systems, wrestling with algorithms that must parse the messy reality of human biology. And as a research affiliate at MIT's Laboratory for Financial Engineering for nearly a decade, I often collaborate with financial engineers and economists, where risk, optimization, and uncertainty are formalized with mathematical precision that could make even a physicist blush.

For some, this portfolio signals restless interdisciplinarity—the academic equivalent of a Renaissance dilettante. I see something else entirely: convergence.

I believe what we call "disciplines" are variations on mathematically-definable themes, each convinced of its own originality. Whether I'm designing clinical studies, analyzing markets, or training models, I'm engaged in identical operations: probabilistic inference, causal reasoning, decision-making under constraints, adaptive learning. In my view, the differences are institutional—and increasingly beside the point.

These are pivotal times. We are living through what can be called the great convergence, as AI reshapes knowledge and dissolves disciplinary boundaries. This isn't hybridization but complete realignment. The problem spaces of science, markets, and computation are fusing, and what I increasingly advocate for is fluency across the mathematical languages that govern uncertainty itself.

I. The 20th century: when knowledge became industrialized

The 20th century industrialized knowledge with ruthless efficiency. Universities carved themselves into departments like assembly line stations. Professional societies erected guild-like barriers with what a colleague recently characterized as "the fervor of medieval craftsmen." Credentialing bodies ensured legitimacy through ritualized gatekeeping. Journals became silos of specialized discourse, readable only by initiates fluent in each field's particular dialect.

This architecture produced immense gains: molecular biology unlocked the genomic revolution, quantitative finance built markets of unprecedented complexity, computer science laid mathematical foundations for today's AI systems. The model worked brilliantly because it matched technological constraints—when information was scarce, computation expensive, and collaboration required physical proximity.

But the model carried three assumptions that have become inconvenient. First, that complex systems could be decomposed into isolated components without losing essential properties. A heart studied independently of the brain, a market independently of regulation, an algorithm independently of deployment context. This worked until we discovered that the most interesting phenomena live precisely in the interactions.

Second, that expertise could be optimized through relentless narrowing of scope. The ideal professional deepened their understanding of increasingly specialized topics, ultimately achieving complete mastery over a very small domain. One might charitably call this intellectual precision; less charitably, it resembles sophisticated myopia.

Third, that progress was primarily intra-disciplinary—that the next breakthrough in oncology would come from oncologists, in finance from financiers, in AI from computer scientists. This assumption has aged about as well as geocentric astronomy.

Many institutions remain trapped in 20th-century organizational logic, like generals fighting with obsolete maps. But the post-Cold War era of stable globalization has fractured. Technology, geopolitics, and economics now form a single, entangled terrain and US–China rivalry plays out in chip fabs and algorithmic supremacy. Central banks pilot digital currencies and biotech companies resemble venture portfolios. Climate solutions demand concurrent advances in materials science, financial engineering, and behavioral economics. The boundaries are vanishing, and with them, the utility of our old maps

II. The deep grammar of uncertainty: a shared mathematical foundation

What we call “disciplines” are often just surface manifestations of deeper, shared mathematical structures. Once we strip away the domain-specific language and institutional packaging, fields like oncology, AI, and finance—through excursions like mine—begin to converge around a common substrate: reasoning and decision-making under uncertainty. This convergence rests on four foundational primitives that together form a shared formal grammar:

1. Probabilistic inference: the universal translator

   At the heart of each domain lies the task of estimating latent states from noisy, incomplete observations. Whether assessing clinical benefit from surrogate endpoints, inferring market direction from price signals, or training a model on limited data, the fundamental operation is the same: updating beliefs via posterior distributions. The observed quantities may vary—PFS curves, asset returns, prediction scores—but the underlying Bayesian mechanics are identical. Across domains, the challenge remains consistent: reconcile prior knowledge with new evidence to distinguish signal from noise in high-dimensional spaces.

2. Causal reasoning

   While probabilistic associations are useful, each field ultimately requires causal inference to support counterfactual reasoning and effective intervention. Clinicians ask whether a treatment causes improvement, investors assess the causal effect of strategies on returns, and ML researchers evaluate whether a model will generalize beyond its training data. These questions invoke a shared set of tools: randomized controlled trials, natural experiments, instrumental variables, and structural causal models. The domain-specific terminology may shift—confounders in medicine, selection bias in finance, dataset shift in AI—but the underlying logic of causal discovery remains the same. The universe appears to be completely indifferent to our disciplinary boundaries.

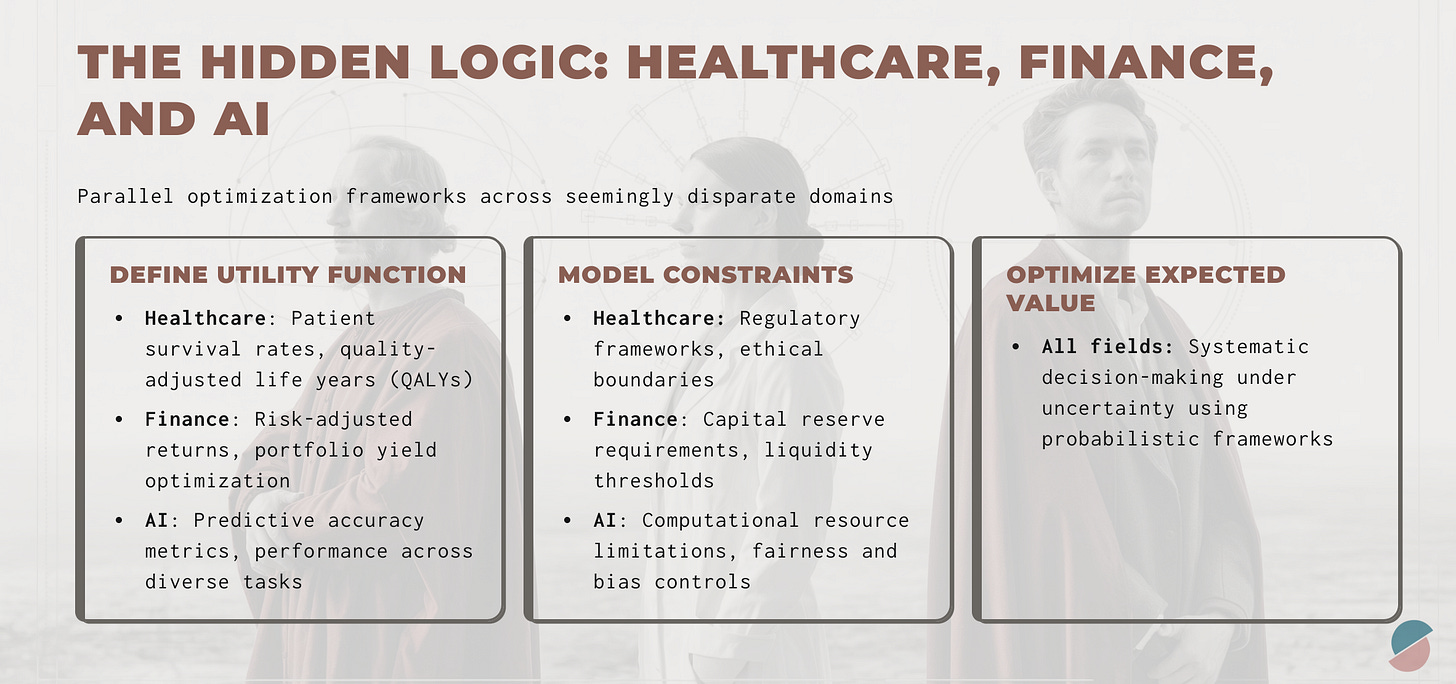
3. Decision theory under constraints

   These domains do not merely aim to model the world—they aim to act within it. Clinical trial design, portfolio construction, and algorithm deployment each involve making decisions under uncertainty subject to real-world constraints. Despite differences in regulatory frameworks (e.g., FDA, SEC) or operational limits (e.g., capital budgets, compute resources), the formal structure is consistent: define a utility function, enumerate constraints, and solve an expected value optimization problem. The domains differ in context, but the decision-theoretic framework remains invariant.

4. Adaptive learning and control

   All three fields operate in dynamic environments where conditions change over time: drug resistance, market regime shifts, and data distribution drift all require continuous model adaptation. Effective strategies balance exploration and exploitation—whether adjusting dosing schedules, reallocating assets, or updating model parameters. These are instances of sequential decision-making under uncertainty, drawing from reinforcement learning, bandit algorithms, and control theory.

What is most striking is not just that these primitives recur across fields, but that their formal representations are increasingly aligned. Bayesian neural networks unify statistical inference and function approximation. Causal machine learning incorporates counterfactual logic into predictive models. The mathematics behind derivative pricing mirrors infectious disease modeling while portfolio optimization and adaptive trial design rely on structurally similar mean-variance formulations.

AI has amplified this convergence by surfacing structural similarities that domain specialists frequently overlook. Language models today can parse regulatory filings from FDA and SEC with comparable fluency and we’ve seen great success with transformer architectures migrating from modeling protein structures to forecasting macroeconomic trends. The same computational constraints—non-stationarity, sample efficiency, generalization under distribution shift—manifest across fields, making clear that barriers between them are institutional rather than epistemic or mathematical.

III. Why convergence matters now: the strategic imperative

The world has become insistent on interconnectedness, turning disciplinary convergence into structural necessity. The 2008 financial crisis, COVID-19 pandemic, and current AI disruption expose a common pattern: our most consequential challenges are inherently systemic, disregarding institutional boundaries between finance, biology, computation, and governance.

In drug development, biomedical innovation can often becine less a scientific problem than a financial one framed in clinical terms. Within venture-backed biotech companies, decisions about which indications to pursue, endpoints to measure, or populations to target can be shaped not only by biological rationale but by capital constraints. Trial duration is bounded by available runway and milestone structures influence what outcomes are measured and when. Indication selection is also guided by anticipated exit strategies. A Phase II study that is scientifically optimal may still be strategically untenable if it exceeds the financing horizon. Understanding clinical trial design in isolation from capital allocation is like optim¹izing engine performance without regard for fuel dynamics—technically feasible but operationally naive.

In AI, similar dynamics apply. Many failures in medical AI do not stem from algorithmic limitations, but from a failure to model the data-generating process with adequate causal precision and appropriate clinical validation due to lack of familiarity of technologists with controlled empiricism². Training data can also be a major problem. For example, electronic health records are not passive containers of clinical truth; they are shaped by reimbursement codes, institutional workflows, and physician behaviors—often optimized for billing, not decision-making. Training algorithms on such data without understanding its provenance results in brittle models that may perform well in isolation but collapse under prospective deployment. The underlying mathematics—Bayesian inference, causal graphs, optimization—may be identical to that used in domains like finance or molecular modeling, but the key differentiator is institutional context. Mathematical competence alone is insufficient without structural understanding of the environment in which the model operates.

This principle also applies in finance. Classical quantitative models, built on assumptions of market efficiency and statistical stationarity, increasingly fail to capture modern financial system dynamics. Today's markets function as complex adaptive systems where participant behavior, institutional incentives, and algorithmic infrastructure co-evolve. Regime changes, non-stationary data distributions, and strategic interactions between agents are not exceptions—they are the norm³. Financial engineering now mirrors AI system design: managing distributed optimization, modeling feedback loops, adapting to data drift, making real-time decisions. The mathematical tools—reinforcement learning, causal inference, probabilistic modeling—are shared across domains. What differs is the institutional landscape in which they are deployed.

Across these examples, the conclusion is consistent: technical methods are portable, but success depends on understanding how they interact with domain-specific structures, constraints, and incentives. The convergence is not just mathematical but also systemic.

IV. The collapse of disciplinary moats

The breakdown of disciplinary boundaries is observable across scientific, financial, and regulatory frontiers, where problems traditionally treated as domain-specific are revealed to be structurally equivalent.

In drug development, competent discovery pipelines now operate under portfolio management logic, routinely applying principles of options theory⁴—originally developed for valuing financial derivatives—to assess R&D assets and inform go/no-go decisions. Adaptive trial designs now incorporate algorithms derived from multi-armed bandit problems, long familiar in reinforcement learning. These developments reflect deeper structural convergence: optimizing a drug pipeline and managing a financial portfolio are mathematically analogous problems, each requiring dynamic allocation of limited resources under uncertainty and time constraints. The variables differ—molecules versus assets, patients versus market signals—but the formal optimization frameworks are identical.

In quantitative finance, the convergence is equally apparent. Modern trading systems increasingly resemble large-scale machine learning architectures. High-frequency trading firms recruit more computer scientists than economists, and neural networks originally designed for language modeling are repurposed for portfolio optimization and market prediction. Risk management systems rely on anomaly detection algorithms also used in cybersecurity. These parallels reflect shared probabilistic foundations: both trading algorithms and ML systems learn latent structure from noisy, non-stationary data to support decision-making under uncertainty. The distinction between financial engineering and machine learning has become largely institutional; mathematically, they are variants of the same inference and optimization problems.

The regulatory domain has followed suit. Whether in drug approval, financial oversight, or AI governance, the underlying challenge remains: how to design institutional mechanisms that align individual incentives with collective outcomes under conditions of asymmetric information, feedback loops, and potential strategic manipulation. Clinical trial protocols aim to minimize bias and ensure generalizability; financial regulations prevent market distortion and systemic fragility; AI standards seek to mitigate risks while preserving innovation. Despite surface differences, each falls within the formal scope of mechanism design—a subfield of game theory focused on optimizing system-level behavior in multi-agent environments (see The Rational Road to Inefficiency below for a game theoretical analysis of government inefficiency).

As these structures converge, the capacity to translate rigorously between them becomes essential. AI has become our most disruptive truth-teller, exposing mathematical unity behind institutional facades and accelerating the collapse of disciplinary boundaries. Large language models read FDA filings and SEC disclosures with comparable fluency, not by memorizing domain-specific jargon but by abstracting shared logical structures. They translate between medical and financial terminology by identifying underlying mathematical relationships—recognizing that clinical trial endpoints and financial metrics both serve as observable proxies for latent risk-return profiles.

What is particularly significant is how AI accelerates real-time methodological convergence across disciplines. Techniques originally developed in one field are rapidly generalized and redeployed elsewhere. Causal discovery methods from econometrics now inform drug target identification. Transformer architectures—initially designed for natural language processing—are routinely applied to protein folding, financial forecasting, and clinical decision support. These migrations reflect shared formal properties of underlying problems: high-dimensional parameter spaces, non-convex optimization landscapes, and non-stationary data environments.

The shared mathematical architecture of decision-making across disciplines. Despite surface differences, healthcare, finance, and AI operate under the same hidden logic: define utility functions relevant to domain goals, model the constraints that shape feasible actions, and optimize expected value using probabilistic reasoning. This framework enables structured, adaptive decision-making under uncertainty.

V. Toward a new model of expertise: the systems architect

What does it mean to be an expert when disciplinary boundaries are increasingly irrelevant? Based on my experience, I believe the dominant mode of expertise must shift. We need fewer narrow specialists and more systems translators: individuals who understand mathematical structures that underpin diverse fields and can apply that understanding across institutional contexts.

Traditional expertise is defined by depth within a silo—accumulating specialized knowledge within bounded domains. By contrast, systems translators develop fluency in abstract patterns that connect domains. This is not generalism or breadth for its own sake, but a different form of depth: the ability to recognize that a phase transition in physics, a regime shift in finance, and a distribution shift in machine learning are formal instances of the same mathematical phenomenon. Surface differences in terminology or institutional setting often obscure deeper structural equivalence.

But abstraction alone is insufficient. Effective systems translation also requires understanding how mathematical structures behave when embedded in specific real-world contexts. The same algorithm—Bayesian optimization, for example—may function very differently depending on institutional environment: regulatory oversight, incentive structures, implementation constraints, and stakeholder dynamics all influence performance. Expertise requires not just theoretical understanding, but the ability to anticipate how formal models interact with complex systems.

This perspective informs how we approach apparent trade-offs. Many decisions that seem constrained by irreconcilable tensions—between efficacy and cost, between speed and safety—are often the result of incomplete or misaligned modeling. Systems translators interrogate the assumptions underlying models themselves: Are we capturing relevant utility functions? Are stakeholder incentives appropriately represented? Is the time horizon correctly specified? In many cases, what presents as hard constraint is instead a product of narrow framing or institutional inertia.

Crucially, systems translators intervene at the level of the system, not just outputs. Rather than optimizing within fixed boundaries, they identify leverage points—feedback loops, incentive structures, information flows—that shape outcomes over time. This orientation is essential for solving problems that are adaptive, emergent, and cross-domain by nature.

This approach is frequently misunderstood as generalism, but the distinction is important. Systems translation does not mean shallow familiarity with many topics. It requires rigorous grounding in mathematical foundations—probability theory, decision theory, optimization, causal inference—combined with deep contextual awareness in multiple domains. It is rare precisely because it cuts across the organizational logic of most institutions. Universities train disciplinary experts. Professional societies certify field-specific competencies. Neither is designed to support expertise that spans both formal structure and institutional application.

Yet as complexity of real-world challenges increases and mathematical frameworks across domains continue to converge, systems translation becomes not just valuable but essential. It enables cross-domain reasoning that is grounded, scalable, and actionable—combining technical precision with systemic understanding. This is the expertise we increasingly need: not to necessarily replace specialization, but to make it interoperable.

AI as a unifying methodological layer across disciplines. Techniques such as causal discovery, transformer architectures, reinforcement learning, and variational inference are creating a shared computational grammar. These approaches are increasingly used to solve structurally similar problems across healthcare, finance, and the life sciences—revealing hidden causal relationships, decoding biological and financial sequences, and optimizing decision-making in complex, resource-constrained environments

VI. The AI acceleration: revealing what was always there

The convergence of disciplines invites a return to something more fundamental than any professional category: reasoning under uncertainty in pursuit of consequential action. This shift is no longer academic—it has become structural necessity with strategic implications. As aging populations strain pension systems, energy transitions demand multidimensional coordination, AI transforms labor markets, and geopolitical competition centers on technological capacity, the ability to synthesize insight across domains is essential for institutional relevance and societal resilience.

Organizations must move beyond the legacy model of hiring narrow specialists and hoping for cross-functional collaboration. Instead, they need individuals with capacity to reason across systems—those who can model interactions between regulatory constraints, financial incentives, technical architectures, and human behavior. Projects should be organized around problem systems rather than disciplinary functions. A drug development initiative should integrate clinical, regulatory, financial, and computational expertise from inception, not assemble them sequentially. The most valuable insights increasingly lie at interfaces—how policy affects technical feasibility, how modeling choices interact with economic incentives, how institutional norms shape data quality.

At the individual level, this shift demands foundational fluency in core primitives that generalize across domains: probabilistic inference, causal reasoning, decision-making under constraints, and adaptive learning. These are not niche technical skills—they are the grammar of systems thinking. Career strategies must reflect this shift. Advancement within a single domain may optimize short-term recognition, but often comes at the cost of long-term relevance. Lateral movement across disciplines, when grounded in deep conceptual continuity, builds translational expertise increasingly needed to navigate complex systems. Understanding mathematical principles that unify machine learning, biostatistics, and financial engineering is more durable—and strategically useful—than mastering the latest toolkits in any one of them.

Institutions must evolve in parallel. Universities should organize around foundational methods—probability, optimization, systems theory—rather than historical departments. Students should learn core concepts in multiple applied contexts: probability theory not just as abstract mathematics, but through clinical trials, market models, and algorithmic learning. Research institutions must develop mechanisms for organizing cross-domain collaboration around problem spaces rather than disciplines. The most urgent questions we face—climate risk, AI safety, biosecurity, economic resilience—require such integration by design.

The transition from disciplinary to systems thinking may not be smooth. Existing professional identities, organizational incentives, and institutional hierarchies remain optimized for 20th-century boundaries. But the shift is already underway, whether or not we formally acknowledge it. The question is not whether convergence will occur—it is whether we will adapt to it intentionally, or be overtaken by it incrementally.

VII. The era of the systems architect and the return of the polymath

We are witnessing the twilight of hyper-specialization precisely when survival depends on synthesis. The disciplinary boundaries that structured 20th-century institutions are dissolving under pressure from mathematical convergence, technological capability, and real-world complexity that refuses to respect departmental org charts.

This is not another call for "interdisciplinary collaboration"—a buzzword that often means putting specialists from different fields in the same room and hoping for synergy. This is recognition of deeper truth: the most consequential problems of our time are inherently cross-systemic and require expertise that transcends traditional boundaries.

I strongly believe that the next generation of innovation will come from systems architects—professionals who combine technical sophistication with institutional fluency, who can model complex systems rather than optimize within silos, who can navigate uncertainty with conceptual precision across multiple domains. This represents a return to an older model of expertise—the polymathic scientist-engineer who could move fluidly between theoretical and practical problems—but with profound depth in technical foundations combined with sophisticated understanding of multiple institutional contexts.

The 20th century gave us the specialist—someone who knew more and more about less and less until achieving perfect knowledge of an infinitesimal domain. The 21st century demands the systems architect—someone who understands deep mathematical patterns connecting apparently disparate domains and can design interventions that work across multiple systems simultaneously.

Organizations and individuals who recognize this convergence earliest will find themselves remarkably well-positioned, while others may discover that deep expertise in a single domain has become the most elegant form of irrelevance. We are no longer in the era of the thoracic oncologist (my speciality), the quant, or the ML engineer. We are in the era of the systems architect—and the future will likely favor those who can see mathematical unity beneath institutional diversity, who can translate between domains with precision and purpose, who can design solutions that work across the full complexity of the real world.

The age of disciplinary sovereignty is ending. The age of systems thinking has begun.

1. See Siah KW, Khozin S, Wong CH, Lo AW. “Machine-Learning and Stochastic Tumor Growth Models for Predicting Outcomes in Patients With Advanced Non–Small-Cell Lung Cancer,” JCO Clinical Cancer Informatics, Volume 3, 2019. (https://doi.org/10.1200/CCI.19.00046). This study, conducted at the FDA with MIT postdocs whose expertise was in mathematics and financial engineering—not oncology or clinical trials—demonstrates just how portable mathematical reasoning is across domains. Their limited biomedical background was no impediment to producing models of remarkable accuracy, underscoring that the grammar of uncertainty is, indeed, a universal language.

2. Controlled empiricism refers to the disciplined application of experimental methods—such as randomized controlled trials or systematic interventions—to generate reliable, reproducible evidence. In contrast to mere observation, it emphasizes deliberate manipulation of variables and rigorous control of confounding factors, ensuring that conclusions are built on more than just the caprice of correlation.

3. “Regime changes” refer to abrupt shifts in the underlying structure or behavior of a system—eg, a market moving from calm to chaos, or a policy upending the rules overnight. “Non-stationary data distributions” describe situations where the statistical patterns of data (like averages or volatility) evolve over time, rendering yesterday’s truths obsolete today. “Strategic interactions between agents” capture the chess-like maneuvers of actors whose choices shape—and are shaped by—each other, creating feedback loops and unpredictability. In short, change and complexity are not the plot twists; they are the plot.

4. Options theory is a branch of financial engineering that quantifies the value of flexibility—specifically, the right but not the obligation to take certain actions as uncertainty unfolds. Originally devised to price financial derivatives, its logic now guides decisions far beyond Wall Street: in R&D, drug development, and even career moves, options theory teaches us that sometimes the smartest play is simply to wait and see. In a world allergic to certainty, optionality can be the ultimate hedge.